RANDOM FATIGUE
Beschreibung der dynamischen Belastung durch PSD (Power Spectrum Density)
In vielen Bereichen der Technik treten regellose Belastungen auf, die jedoch mit Hilfe statistischer Analysen beschrieben werden können, da gewisse Regelmäßigkeiten auftreten.
So haben Untersuchungen an Flugzeugen, Schiffen oder Straßenfahrzeugen gezeigt, dass die Anregung bei bestimmten Frequenzen besondere Intensitäten aufweist und mit Hilfe des Leistungsdichtespektrums beschrieben werden kann. Mit der Finiten Elemente Methode ist es vergleichsweise einfach möglich, das Verhalten von Strukturen unter Anregung durch ein Leistungsdichtespektrum zu bestimmen.
Damit bietet sich eine vergleichsweise einfach durchzuführende Strukturanalyse an, die gegenüber der statischen Analyse den entscheidenden Vorteil hat, dass die dynamischen Systemeigenschaften in Abhängigkeit von den anregenden Frequenzen berücksichtigt werden.
Zunächst soll der einfachste Fall einer stochastischen Anregung in nur einer Richtung beschrieben werden. Gleichzeitige Anregungen in mehreren Richtungen verlaufen prinzipiell ähnlich und werden nachfolgend behandelt.
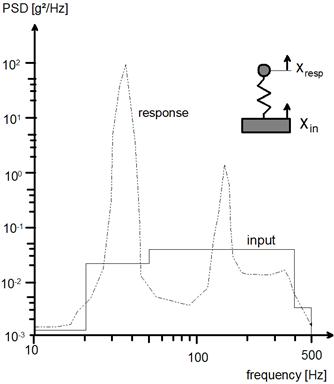
Ein Beispiel für eine typische Darstellung zeigt die Abbildung oben. Dort ist die Leistungsdichte (Power Spectrum Density) einer Systemanregung xin (z.B. Anregung eines Schwingtisches, input) und einer Systemantwort der Beschleunigung (Bewegung eines Punktes der gemessenen Struktur, response) in g²/Hz über der Frequenz dargestellt. In der Realität ist anstelle einer Punktmasse die zu prüfende Struktur auf einem Prüftisch befestigt.
Reale Strukturen haben - im Gegensatz zu einer Punktmasse - eine Vielzahl von Punkten mit unterschiedlichen Bewegungen, für die jeweils ein Leistungsdichtespektrum der Beschleunigung gemessen und auch berechnet werden kann. Auch die auftretenden Spannungen können für jeden Punkt als PSD dargestellt werden, auf deren Basis eine Lebensdauerberechnung durchgeführt werden kann.
Die praktische Vorgehensweise bei der Lebensdauerberechnung ist im folgenden Ablaufschema dargestellt. Dabei wird davon ausgegangen, dass das zu untersuchende Bauteil auf einem Rütteltisch angeordnet ist, der als Starrkörper angenommen wird.

Experimentelles Verfahren
Bei einem experimentellen Verfahren wird z.B. ein Schwingtisch verwendet, auf dem die zu prüfende Struktur befestigt wird. Für den Schwingtisch wird ein Leistungsdichtespektrum als Anregung vorgegeben und das daran befestigte Bauteil wird an seinen Kontaktstellen mit dem Schwingtisch entsprechend beschleunigt.
In Normen für den Schiffsbau, den Flugzeugbau oder für elektronische Bauteile findet man solche Leistungsdichtespektren, auf deren Grundlage wichtige Prüfverfahren definiert sind, die das Bauteil ohne Schaden überstehen muss.
Natürlich ist es auch möglich, das Bauteil bis zum Versagen zu prüfen und damit ein experimentelles Ergebnis für die Lebensdauer zu erhalten. In der Regel wird das Bauteil jedoch nicht bis zum Versagen gefahren, sondern nur der erfolgreiche Nachweis der Betriebsfestigkeit durch das schadensfreie Überstehen der Prüfung erbracht. Um eine Abschätzung der Sicherheit zu erhalten, wird bei diesem Versuch häufig der „Lebensdauerverbrauch“ berechnet. Dazu werden die Dehnungen an den gefährdeten Stellen gemessen und diese Daten für eine Lebensdauerberechnung verwendet. Die gemessenen Dehnungsverläufe über der Zeit oder das Leistungsdichtespektrum der gemessenen Dehnung (Spannung) bilden die Grundlage für eine Lebensdauerberechnung.
Rechnerischer Ansatz
Der experimentelle Ansatz kann vollständig durch rechnerische Verfahren ersetzt werden. Dazu wird ein FE-Modell der Struktur erstellt und die Anregung durch die Beschleunigung rechnerisch simuliert. Die Vorgabe der Beschleunigung erfolgt - analog zum experimentellen Vorgehen - ebenfalls über das Leistungsdichtespektrum der Beschleunigung in g2/Hz.
Für das System werden dabei die Eigenfrequenzen und Eigenformen berechnet. Sie stellen wichtige Zwischenergebnisse dar, die eine Plausibilitätskontrolle ermöglichen. Wichtig ist, dass alle Massen und Steifigkeiten korrekt eingegeben werden.
Als Ergebnis erhält man dann für jeden Knoten der FE-Struktur die RMS-Werte der Spannungen für einen bestimmten Frequenzbereich und kann daraus das Leistungsdichtespektrum der Spannungen in MPa2/Hz bestimmen.
Aus dem Leistungsdichtespektrum der Spannungen kann nun für jeden Knoten eine Häufigkeitsverteilung der Spannungsamplituden berechnet werden, die dann als Basis für eine Lebensdauerberechnung verwendet wird (siehe obiges Ablaufschema).
Chrakteristische Kenngrößen eines dynamischen Systems
Eine sehr wichtige elementare Kenngröße ist der Effektivwert oder auch RMS-Wert (=Root Mean Square) genannt, der wie folgt definiert ist:
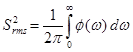
Die stochastischen Kenngrößen können auf die Frequenz f in der Einheit Hz oder auf die Kreisfrequenz in der Einheit 1/s bezogen werden. Der Zusammenhang zwischen Kreisfrequenz und Frequenz ist gegeben durch:
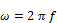
Das Quadrat des Effektivwertes entspricht der Fläche unter der Leistungsdichtekurve. Weitere wichtige Kenngrößen für das Schwingungsverhalten sind durch die Momente der spektralen Dichte gegeben (siehe Abbildung).
Zu ihrer Bestimmung ist das Flächenelement Ø(f)df mit dem „Hebelarm“ fn zu multiplizieren. Für das Moment Hn nullter Ordnung ist n=0, erster Ordnung n=1 , usw. bis n=4.
Entscheidend ist nun, dass mit diesen Momenten H0,H1,H2,H3,H4 die folgenden wichtigen Kenngrößen bestimmt werden können:
- Effektivwert wie oben
- Zahl der Nulldurchgänge pro Sekunde
- Anzahl der Spitzenwerte pro Sekunde (entspricht der Schwingspielzahl pro Sekunde)
- Unregelmäßigkeitsfaktor I

Eine Einteilung des dynamischen Systemverhaltens anhand des Ungleichförmigkeitsfaktors ist möglich, wobei die folgenden vier Fälle unterschieden werden, wie in der Abbildung dargestellt.

Unter der Voraussetzung, dass das Systemverhalten stochastisch, stationär und ergodisch ist, kann in Abhängigkeit vom Ungleichförmigkeitsfaktor das geeignete Verfahren zur Berechnung des Amplitudenkollektivs gewählt werden.
Sinuskurve mit konstanter Amplitude und Frequenz (I=1)
Da es sich nicht um einen stochastischen Prozess handelt, sind die nachfolgend beschriebenen Methoden zur Kollektivbildung nicht geeignet. Stattdessen liegt ein deterministisches Verhalten vor und es kann auf einfache Weise ein Einstufenkollektiv bestimmt werden.
Schmalband-Prozess (I~1)
Die Verteilung wird nach folgender Gleichung berechnet:
![]()
![]()
Dabei ist S die Schwingweite, also die doppelte Amplitude. Der Index NB steht für Narrow-Band.
Breitband-Prozess (0<I<1)
Die Berechnung der Verteilung erfolgt nach Dirlik [ ] gemäß folgender Gleichung:
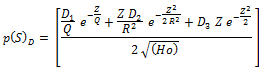
mit
Z = ![]() I =
I = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dabei ist S die Schwingweite also die doppelte Amplitude.
Ablauf der rechnerischen Analyse
Vorgabe der Anregung für den Schwingtisch:
Berechnung der Eigenformen und Eigenfrequenzen des Systems (Modalanalyse) mit Hilfe FEM
Berechnung der Systemantwort (Leistungsdichtespektrum der Spannung für jeden Knoten)
Bestimmung eines schädigungsgleichen Kollektivs
Durchführung einer Lebensdauerberechnung
Ein Beispiel mit FEMAP zeigt die Vorgehensweise im Detail.